Свойства последовательного соединения КАМСИ
Рассмотрим последовательное соединение двух КАМСИ А1 и А2 (см. Рис. 5). Выше, на стр. 38 (см. Рис. 3) мы уже рассматривали последовательное соединение двух КАМСИ, кодера и декодера, которые соединены информационным каналом. Теперь мы рассмотрим такое объединение конечных автоматов, которое интересует нас постольку, поскольку его можно заменить эквивалентным конечным автоматом. Нас интересует способ построения такого автомата и его свойства и параметры.
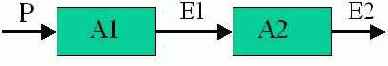
Рис. 5
Докажем следующее утверждение.
Утверждение 1 Композиция двух последовательно включенных КАМСИ А1=>А2 (Рис. 5) является КАМСИ, которая имеет порядок ?= ?(A1) + ?(A2), где ?(A1) и ?(A2) - ?-порядки КАМСИ А1 и А2, соответственно
Доказательство. Из определения КАМСИ следует, что ?(A1) символов входного потока битов (Р), поданных на вход КАМСИ А1 достаточно, чтобы определить первый символ Р на выходе Е1. Однако, на выходе Е2 он может появиться только через ?(A2) битов
Е1 на входе КАМСИ А2. Отсюда следует, что первый символ Р на выходе Е2 может быть получен после ?= ?(A1)
+ ?(A2), символов, поданных на вход Р, то есть, композиция КАМСИ А1,А2 также является КАМСИ и имеет порядок ?= ?(A1) + ?(A2).
Пример 2
В Table 2(a) и (b) приведены таблицы переходов КАМСИ А1 и А2 µ-порядка 2, а в Table 2(c) и (d) – инверсные им автоматы SS1 и SS2, соответственно ([30]).
|
А1 |
P,E | ||||
|
P=0 |
P=1 | ||||
|
A |
B,0 |
A,0 | |||
|
B |
A,1 |
B,1 | |||
(a)
|
А2 |
P,E | ||||
|
P=0 |
P=1 | ||||
|
A |
A,1 |
B,1 | |||
|
B |
B,0 |
A,0 | |||
(b)
?(A1) = 2
SS1
P,E
E=0
E=1
S0
S1,1
S2,1
S1
S1,1
S2,1
S2
S3,0
S4,0
S3
S1,0
S2,0
S4
S3,1
S4,1
(c)
|
SS2 |
P,E | ||||
|
E=0 |
E=1 | ||||
|
S0 |
S1,0 |
S2,0 | |||
|
S1 |
S1,0 |
S2,0 | |||
|
S2 |
S3,1 |
S4,1 | |||
|
S3 |
S1,1 |
S2,1 | |||
|
S4 |
S3,0 |
S4,0 | |||
(d)
Table 2
Обозначим через А1 и SS1 кодер и декодер, соответственно, (аналогично А2 и SS2). В Table 3 и в Table 4 (строка (а)) приведен один и тот же поток Р бит (кодируемый текст, который известен только отправителю, см. Table 3(а)). В строках (b) таблиц приведены состояния, в которые переходят автоматы А1 и А2, соответственно. В строках (с) – значения на выходе – закодированный текст, который может быть известен всем. В строках (d) и (e) приведены результаты декодирования, которые показывают, что результаты декодирования совпадают с исходным текстом, но появляются, начиная с третьего бита, то есть, с задержкой, равной двум.
Table 5
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|||||
A1 |
A |
A |
A |
B |
B |
A |
B |
B |
B |
A |
B |
B |
A |
B |
B |
B |
B |
|||
E1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
1 |
||||
A2 |
A |
A |
A |
A |
B |
A |
A |
B |
A |
B |
B |
A |
B |
B |
A |
B |
A |
|||
E2 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
||||
SS1 |
S0 |
S2 |
S4 |
S4 |
S4 |
S3 |
S2 |
S4 |
S3 |
S2 |
S3 |
S1 |
S2 |
S3 |
S1 |
S2 |
S3 |
|||
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|||||
SS2 |
S0 |
S2 |
S3 |
S2 |
S4 |
S3 |
S1 |
S1 |
S2 |
S3 |
S1 |
S1 |
S2 |
S3 |
S1 |
S2 |
S3 |
|||
0 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|||||
Table 6 |
||||||||||||||||||||
Из приведенных примеров и Утверждений 1 и 2 можно вывести следствие: если последовательность автоматов состоит из m компонентов, то они представляют собой КАМСИ-композицию µ-порядка, равного
?= ?(1)… +.. ?(i)…+… ?(m); (i:=1,m) Форм. 8 .